Category: simulations
-
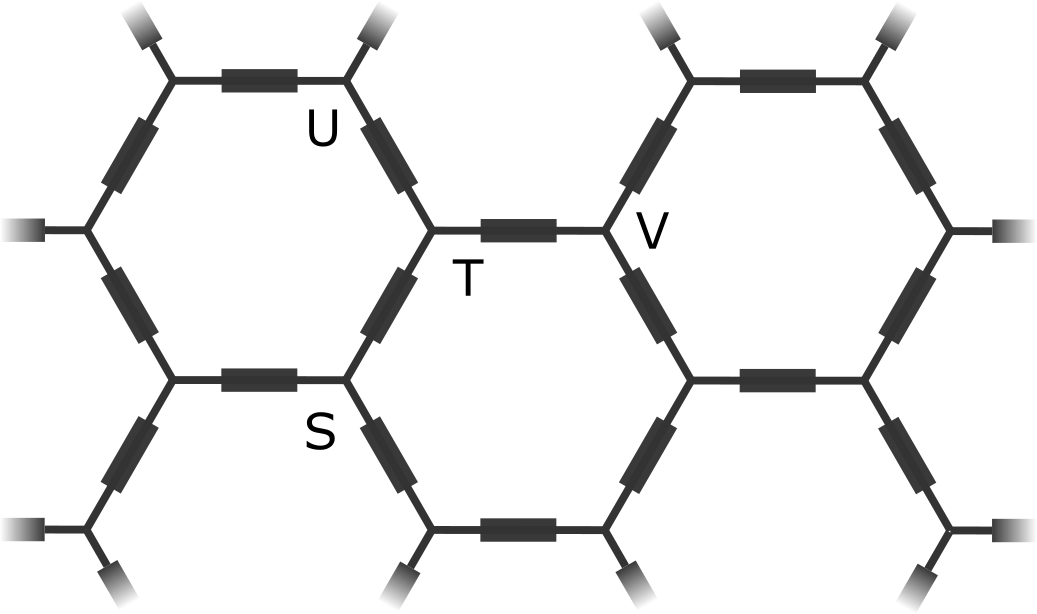
The case of the infinite hexagonal resistor network
I was thinking again about infinite resistor networks and curious to extend the analysis from a square to a hexagonal resistor network. See this previous post for a discussion of the nerd-sniping problem. In particular I was interested in the ‘obvious’ resistances that crop up. For example, in the following square network of 1 Ω…
-
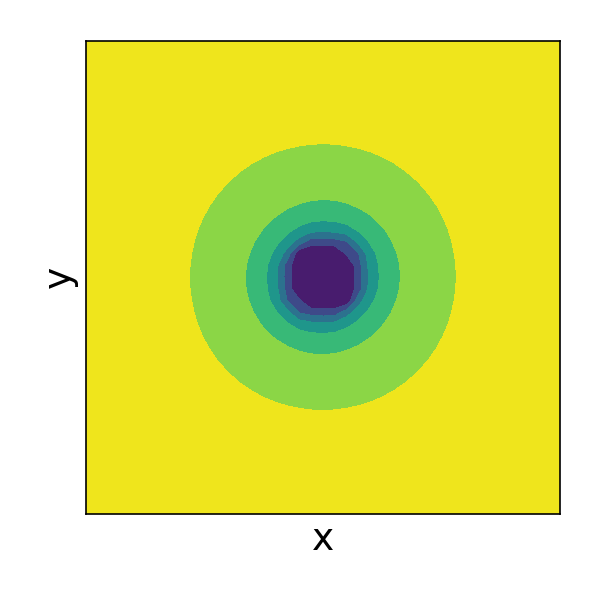
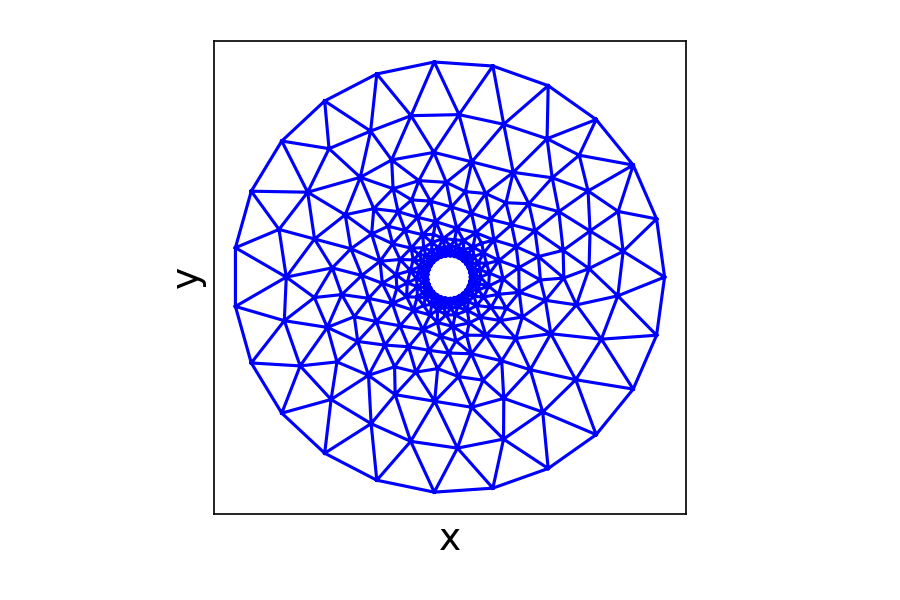
The diminishing returns of stoma density (part 2)
I develop a simplified 3D model of a stoma, building on my previous 2D simulation. The overall aim is, by simulation, to understand stoma density on the underside of a leaf. As before, I am going to use the open-source finite element package FEniCS. The FEniCS experience provides quite a contrast for those of us…
-
The diminishing returns of stoma density (part 1)
Imagine that you were in the business of designing leaves. What stoma density would you choose? Too few and your leaf will not take in enough carbon dioxide. Too many and you will unnecessarily increase the leaf’s complexity. You can imagine other related questions. Why does a bacterium have a certain number of chemo-receptors? The…
-
Benchmarking matrix equation solvers – Python (SciPy) vs. Julia
I am often tempted to try the programming language Julia for scientific computing. It promises fast execution and relative ease of operation: it can run in a Jupyter notebook and is dynamically typed. Furthermore, it has a growing number of well-reviewed packages, including for differential equations and machine learning. In this blog-post I am going…
-
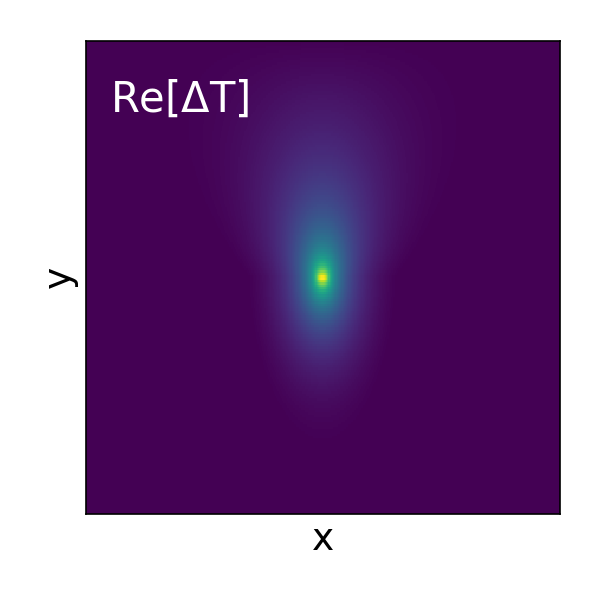
Simulating measurements of thermal conductivity
The 3-omega method provides a widely employed measurement of thermal conductivity. Omega (ω) is the angular frequency (ω = 2πf) of electrical current applied through a wire patterned on a substrate. An attractive feature is that the technique doesn’t suffer significant errors from black-body radiation, as long as the excited temperature rise is small. Moreover,…
-
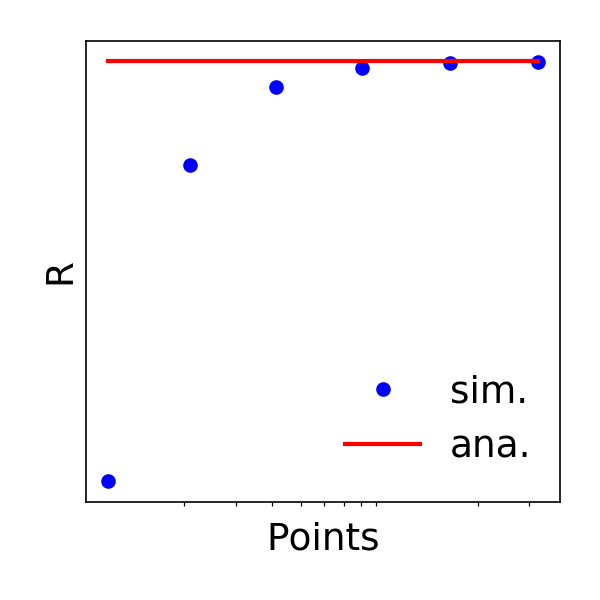
Points on the infinite resistor grid
Nerd Sniping is one of my favourite XKCD comics. It deals with being absorbed in an interesting maths/physics/engineering problem and totally ignoring the real world – to potentially disastrous consequences. In this case, the question is to find the electrical resistance between two specific points on an infinite resistor grid. Embarrassingly, I even fell victim…
-
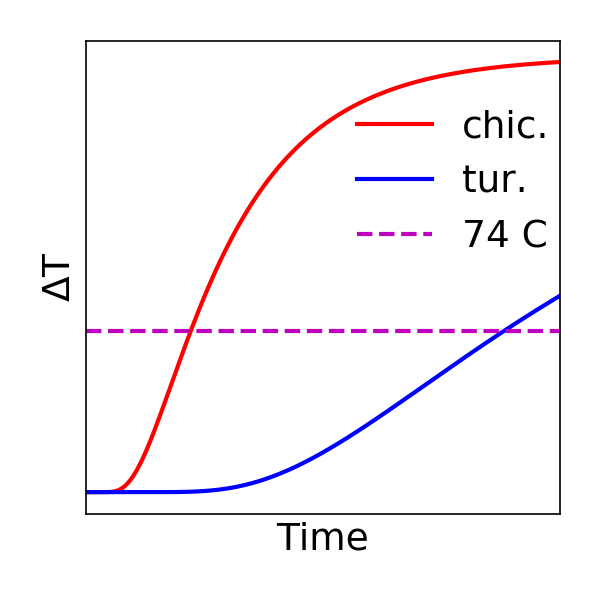
Cooking turkeys and chickens
A while ago now I applied for an undergraduate place to study physics at the University of Oxford. In the interview I was asked a question about the relative cooking times of chickens and turkeys. My reasoning at the time was that heat went in at the surface but needed to raise the temperature of…
-
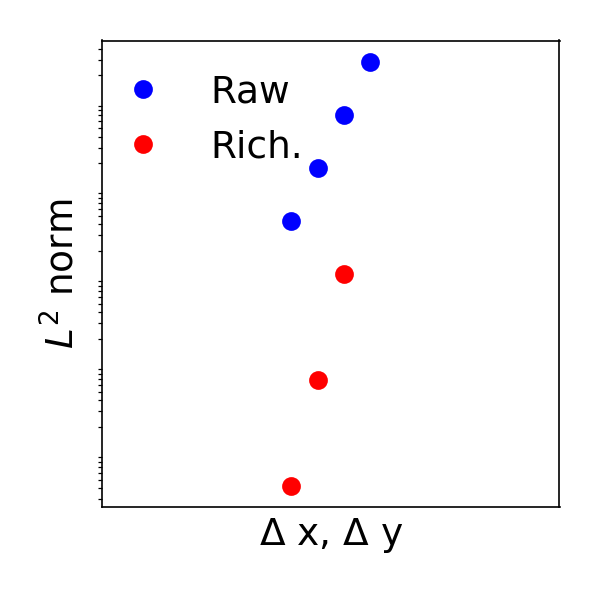
Richardson extrapolation
I wanted to run through an example of how to increase simulation accuracy using the well-known technique of Richardson extrapolation [1]. The main idea is that the difference between the exact solution to a PDE and an approximate numerical solution can be written as a power series in , the step size. If, for example,…