I develop a simplified 3D model of a stoma, building on my previous 2D simulation. The overall aim is, by simulation, to understand stoma density on the underside of a leaf. As before, I am going to use the open-source finite element package FEniCS. The FEniCS experience provides quite a contrast for those of us that have had the tricky task of populating new matrices as we take a simulation from 2D to 3D. In FEniCS the symbolic definition of the PDE doesn’t change. The dimensionality of the simulation is defined by the dimensionality of the mesh that we pass into the solver. Much easier, though of course the mesh is more time-consuming to define in 3D.
Model
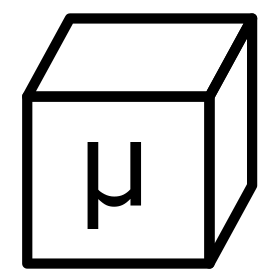
The simulation domain is a cube of length L = 200 µm on each side. The upper and side faces take a constant value for n of 1 /µm3. The variable n ultimately represents carbon dioxide density but I’m still using arbitrary rather than real units. The natural spatial units of the simulation are µm, due to typical stoma dimensions (diameter < 100 µm). In general a stoma has an elliptical shape, but for now we will keep it circular. In the simulation below, I choose a diameter 2r0 = 30 µm. Within this circle, which sits on the bottom face of the domain, the density n is set to zero, modelling a perfect absorber. And the rest of the bottom face has a zero derivative boundary condition set. The only place that can absorb is the stoma. This is a boundary value problem – we find the equilibrium solution without having to know its time-dependence.

The equation is the familiar diffusion equation with no source terms – i.e. the Laplace equation, as below. The simulation code can be found in the following repo.
\( D \nabla^2n = 0\)
Simulation results
We first take a qualitative look at the simulation results. From taking a cross-section in the x-z plane (at y = 100 µm) we see contours in density as one might expect around a perfect absorber (below left). And related behaviour (below right) is observed in the x-y plane (at z = 0 µm). The characteristic length-scale in both cases is around the diameter of the stoma.


And we can quantify the behaviour by fitting to line traces through the 3D density data. In the vertical direction (below left), centred on the absorber, a fit to an exponential rise, \( n(z) = 1 – exp(-z/a)\), gives us a critical length-scale of a = 22 µm. Performing a similar fit in the x-direction (below right) we get a = 17 µm, though in that case we can see that the proximity of the boundaries are perturbing the result (there is a non-zero gradient at the boundary).

Flux and current
From Fick’s first law we can get the flux and then the total current through the stoma. For comparison, there is an analytic expression for the current to a perfect absorber in a semi-infinite volume (see Random Walks in Biology by Howard Berg). In the following expression for the current, I, we find the density n0 (1/µm3) far away from the absorber, the diffusion coefficent D and the radius, r0 (15 µm). Let’s define D to be 1 µm2/s for convenience. Then we see that I = 60/s.
\( I = 4Dn_0r_0\)
Now from the simulation data we can determine the current density (or flux) in the vertical direction from the following expression.
\(j = -D \frac{\partial n}{\partial z}\)
Plotting the magnitude of the flux at z = 0 µm we see the following colourmap, again using a value of 1 µm2/s for D. As expected, the current density peaks in the region of the stoma. The ring effect, where the current density is highest around the perimeter, is likely real. The area elements around the perimeter face less competition than the ones in the middle for diffusion current.
When the current density is integrated over the area, we find I = 67 /s. This is 10 % larger than predicted by the analytic expression. The discrepancy is possibly explained by the course gridding and/or relatively close boundaries.

Discussion
I was quite happy with this simple model, though I would liked to have seen closer agreement between the analytic expression for current and our simulated value. This needs to be investigated before we go onto a larger simulation domain with multiple stoma. Also, we will have to watch carefully the effect of the boundaries on the absorber and ensure that they are not causing a significant perturbation to the carbon dioxide density around the stoma.