Imagine that you were in the business of designing leaves. What stoma density would you choose? Too few and your leaf will not take in enough carbon dioxide. Too many and you will unnecessarily increase the leaf’s complexity. You can imagine other related questions. Why does a bacterium have a certain number of chemo-receptors? The surprising answers to these questions are reviewed in Prof. Berg’s book, Random Walks in Biology (see previous post).
Beyond a certain density of stoma (or chemo-receptors) there is little value in adding more. The diffusion equation shows us that the additional stoma sit in the depletion zone of the others. Hence, they are unable to successfully absorb carbon dioxide. It is a classic case of diminishing returns. I am keen to simulate this interesting problem but let’s build up to it over a series of posts. I start with a simple 2d problem of a circular absorber. In this case, there is a simple analytic solution providing a useful checkpoint.
Method
I’ll use FEniCS, an open source finite element package, to simulate the diffusion equation. FEniCS runs in a Docker container and has a high-level Python interface conveniently enabling it to run in a Jupyter notebook. To create the mesh, I use Gmsh, another open source package. And, using Python, I perform analysis of the results in a Jupyter notebook. All the code can be found in this repo.
The model
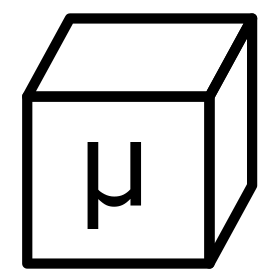
Somewhat arbitrarily I chose a 100 μm radius disc as the simulation domain. A constant value of density (1 per μm2), perhaps of carbon dioxide, is set on the outer boundary. The absorber (say a stoma) is a 10 μm radius disc in the centre of the domain. It too has a constant boundary condition (0 per μm2), corresponding to being a perfect absorber.

The simulation
A simulation gives us the following result for density throughout the domain. It is much as expected and a quick glance shows that the boundary conditions are indeed satisfied.

We had better check the result against an analytic solution. It’s easy enough in this case. We can just integrate the radial equation of the Laplacian in cylindrical coordinates. The result is of the form \( u(r) = A \ln(r)+ B\), with the coefficients A and B set by the boundary conditions. Below I plot the simulation and the analytic expression. Clearly, there is good qualitative agreement. And the L2 norm of the data is 0.002, giving us a quantitative handle to optimise grid density, if required.

Discussion
This was a simple start but provided us the chance to think about the boundary conditions. We’ll continue to use a perfect absorber and also a constant density on the perimeter of the domain. Clearly, we’ll need to think about the domain size, so the proximity of the perimeter doesn’t affect the density around the stoma. Next time, we move to 3d and do a similar check against an analytic result.