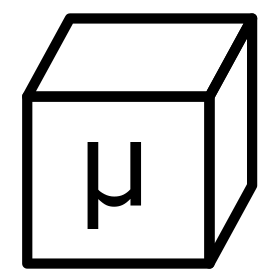
The 3-omega method provides a widely employed measurement of thermal conductivity. Omega (ω) is the angular frequency (ω = 2πf) of electrical current applied through a wire patterned on a substrate. An attractive feature is that the technique doesn’t suffer significant errors from black-body radiation, as long as the excited temperature rise is small. Moreover, the samples are relatively easy to pattern and the equipment needed (a lock-in amplifier) is widely available. The original paper by Prof. Cahill of the University of Illinois (RSI, 1990) provides a great introduction. I am a big fan of this work due to its elegance, usefulness and relative simplicity.
In this blog-post, we perform a simulation in Python of the thermal field that results from passing an oscillating current through a metal wire on a glass substrate. Looking at the amplitude of the local temperature variation at the surface, we will then be able to extract the thermal conductivity, following the 3ω methodology. The actual 3ω technique differs from this simulation by using frequency-mixing in the heater itself to determine the amplitude of temperature variation. It is this frequency mixing, leading to a voltage term at 3ω, that provides the method’s name.
How the experimental technique works
Measurement of thermal conductivity
According to Carslaw and Jaeger’s book (Conduction of Heat in Solids), the temperature at a radial distance r from an infinitesimally wide wire on a semi-infinite substrate is as follows.
\(\Delta T = \frac{P}{2\pi\kappa}K_0(qr)\)
In this expression K0 is the modified zero order Bessel function; P is dissipated power per unit length and κ is the thermal conductivity. The complex wavevector \(q = \sqrt{\frac{2i\omega}{D}}\), where D is thermal diffusivity and ω is angular frequency. The key result, that makes it clear how we can extract thermal conductivity, is the approximation to ΔT for qr << 1. Of course this is only for an infinitesimal wire, but it shows the principle. For wider wires we need to evaluate an integral (Cahill, expression 8).
\(\Delta T = \frac{P}{2\pi\kappa}(\frac{1}{2}ln\frac{D}{r^2}+ ln2 -0.5772- \frac{1}{2}ln(2\omega) – \frac{i\pi}{4})\)
Looking at the gradient of temperature amplitude with angular frequency, we find the following expression. It allows us to determine κ in terms of measured (the gradient) and known (the power per unit length) quantities.
\(d\Delta T/d(ln(2\omega)) = P/4\pi\kappa\)
The frequency mixing
An alternating current (at angular frequency ω) passes through a narrow electrical wire, and leads to power dissipation at angular frequency 2ω. There is a corresponding variation in temperature at the wire itself at angular frequency 2ω. Since electrical resistance increases with temperature (for a metal) there is also now a variation in electrical resistance at angular frequency 2ω. To recap, the current is at angular frequency ω and there is a component of resistance at angular frequency 2ω. Hence we end up, via Ohm’s law, with a voltage component at an angular frequency 3ω. This voltage at angular frequency 3ω tells us about the temperature variation at the wire. We can then analyse this as a function of ω and determine κ as previously mentioned.
Setting up the simulation
First, let’s consider the heat diffusion equation with a sinusoidal source term. Previously we looked at the heat diffusion equation in the time-domain but this will be a frequency domain approach. The specific heat capacity is given by c and the density by ρ.
\( \kappa \nabla^2T = c\rho\frac{\partial T}{\partial t}-qe^{-i\omega t}\)
Let’s assume that we are interested in the temperature response at the same frequency as the driving frequency i.e. \(T = T e^{-i\omega t}\). Substituting this in, it is clear that we lost the explicit time-dependence, leaving us with an equation similar to the Poisson equation.
\( \kappa \nabla^2T = -i \omega c \rho T-q\)
We show the details of finite differencing in the GitHub repository for this post. In brief, we integrate the equation and use the divergence theorem to eliminate the second derivative. We want to be able to vary the thermal conductivity across the domain and the thermal conductivity matrix is set-up on a staggered rectangular grid (staggered by half a lattice spacing from the temperature grid). Finally, we end up with a sparse matrix equation that we can solve directly using SciPy sparse matrix methods.
The thermal conductivity is chosen to represent a glass wafer (κ = 1.3 W/m/K) covered by air (κ = 0.025 W/m/K). And for the wire we use a width of 20 µm and a height of 2.5 µm. The number of grid points in x (y) is nx = 401 (ny = 201). The wire width is representative of one patterned by optical lithography. The height, however, is thicker than is usual for a deposited thin film.


The simulation
Using Python we solve the matrix representation of the finite difference equation. We are able to find the complex temperature response at a given frequency of excitation, here 1000 Hz. The real part, Re[ΔT], gives the response in-phase to the driving power. And the imaginary part of the response, Im[ΔT], gives the out-of-phase response. It is interesting to consider the thermal wavelength \(\lambda = |\sqrt{D/2i\omega}|\). At 1000 Hz, and in glass, \(\lambda = 6 \mu m\). This appears consistent with the spatial distribution of temperature seen in in the simulation of Re[ΔT].


In the 3ω experiment, and likewise in the simulation, we are interested in the average temperature over the heater. Plotting this average temperature as a function of frequency we obtain the data points in the following graph. Also plotted is the (numerically integrated) integral, giving the expected real temperature response (Cahill, equation 8). The slope appears correct however the absolute value is offset from the data. This needs further investigation, however for the measurement of thermal conductivity it is the slope that is important.

We take a closer look at that slope, fitting all data points to determine the gradient. From the gradient and the expression for the \(d\Delta T/d(ln(2\omega)) \) we can extract a value of, κ, the thermal conductivity. We find that κ = 1.39 W/m/K, approximately 10% greater than the value for glass (κ = 1.3 W/m/K) used in the simulation. Why might this discrepancy arise? The analytic expression for the gradient is valid in the case that the thermal wavelength is much greater than the wire width. And we already saw that this constraint is not satisfied at 1000 Hz, where that wavelength (6 µm) is already less that the wire width (20 µm). If we fit only up to 100 Hz, rather than all the data points, we find a closer match, with κ = 1.34 W/m/K.

Conclusions
In simulating the thermal part of the 3ω technique we have seen some of the frequency constraints that exist due to the thermal wavelength. It will be interesting to understand where the errors in approximating the PDE by a difference equation contribute to the discrepancy between the simulated and expected values of κ. This could readily be achieved by performing a convergence analysis. I am also looking forward to examining the high and low frequency limits in more detail. Finally, it will be fun to try to see how accurately it is possible to get the fitted and input values of thermal conductivity to match.