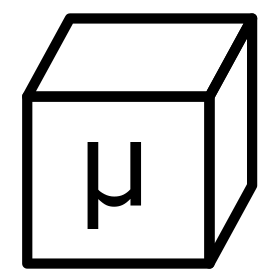
I wanted to run through an example of how to increase simulation accuracy using the well-known technique of Richardson extrapolation [1]. The main idea is that the difference between the exact solution \(u_a\) to a PDE and an approximate numerical solution \(u(h)\) can be written as a power series in \(h\), the step size.
\( \begin{equation}
u_{a} = u(h) + g_1 h + g_2 h^2 + …
\end{equation} \)
If, for example, it is known that the leading error term goes like \(h^2\) then \(g_1 = 0\). By taking two numerical solutions with different values of \(h\), it is possible to write a pair of linear equations with two unknowns: \(u_a\) and \(g_2\). Eliminating \(g_2\), we get \(u_a\) – an improved approximation to the PDE.
In this example, I use a central difference approximation to the Poisson equation, with leading error term that goes like \(h^2\).
\( \begin{equation}
\nabla^2 u(x,y) = -\rho (x,y)
\end{equation} \)
Using the method of manufactured solutions, I choose a solution \(u_a\) and by differentiation determine what the source term \(\rho(x,y)\) must have been. This source term is then used for the numerical solution. The simulation domain is taken as being a rectangle defined by the pair of points \((0,0)\) and \((L_x,L_y)\).
\(\begin{equation}
u_a = \sin(\frac{\pi x}{L_x})\sin(\frac{2 \pi y}{L_y})
\end{equation}\)
The finite difference equation is as follows:
\(\begin{equation}
\frac{u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{\Delta x^2}+\frac{u_{i,j+1}-2u_{i,j}+u_{i,j-1}}{\Delta y^2} = -\rho_{i,j}
\end{equation}\)
It is written as a sparse matrix equation and solved directly using SciPy’s spsolve method. In this way we find the numerical solution which can be compared to the analytic solution. The right-hand figure shows a slice through the colourmaps at x = 0.5. The Python code for this simulation is available in a GitHub repository.

Of course it is not enough to perform a visual comparison so the \(L^2\) norm is used to compare the two.
\(\begin{equation}
L^2 = \sqrt{\Sigma (u-u_a)^2/\Sigma u_a^2}
\end{equation}\)
By plotting the \(L^2\) norm as a function of \(\Delta x = \Delta y\) we can see the second order convergence, as expected, from this numerical approximation to the Poisson equation. In fact, a linear fit to the base-10 log of these data points gives a convergence rate of 2.0.

Finally, we are in a position to consider Richardson extrapolation. For a numerical approximation \(u(2h)\) and \(u(h)\) the extrapolated solution can be written as follows. Note that the discretisation parameter is chosen so that there are common grid points in \(u(2h)\) and \(u(h)\).
\(\begin{equation}
u_R = 4/3 u(h) – 1/3 u (2h)
\end{equation}\)
So from a pair of numerical solutions we deduce a single extrapolated solution, \(u_R\). These are plotted vs \(h\) as the orange points in the following graph, the blue points being the raw solutions. A remarkable decrease in \(L^2\) norm is seen, but not only is there a decreased \(L^2\), there is also a gain in convergence rate to 4.0 as determined by a fit. Essentially we have removed the second order error term, and since there is no third order term in the central difference approximation to the second derivative, we are left with a fourth order error term.

The benefit of Richardson’s extrapolation is clear, it provides an advantage in accuracy in the case that there is a well known rate of convergence, and that there are common points on a structured grid. The article by Roache provides a clear description of the extrapolation technique and its use [2]. This tutorial also provides more details about the implementation.
[1]: L. F. Richardson, Trans. R. Soc. London Ser. A (226) 229 (1927).
[2]: P. J. Roache, Annu. Rev. Fluid. Mech., (29) 123 (1997).