Nerd Sniping is one of my favourite XKCD comics. It deals with being absorbed in an interesting maths/physics/engineering problem and totally ignoring the real world – to potentially disastrous consequences. In this case, the question is to find the electrical resistance between two specific points on an infinite resistor grid. Embarrassingly, I even fell victim to it when one of my electronic engineering colleagues (thanks Robert!) wrote the circuit on a whiteboard at work. I then spent a few hours finding a numerical solution to the problem. Actually, while the analytic solution is more beautiful, it is interesting to solve numerically. The matrix equation ends up being the same as that required to solve the Poisson equation. In this post, I run through that finite difference solution. But first, let’s take a look at the Nerd Sniping comic.

Setting up the problem
To perform an experimental measurement of the resistance between two points in the resistor grid we would attach our multimeter probes and read off the resistance. I imagine that the multimeter passes a known current between the probes and then measures the voltage dropped across them, allowing the resistance to be determined. Let’s take the same approach and apply a current source at the first node and an equivalent current sink at the second node. In fact, we can consider there to be current source (of positive or negative value) at each node, but in almost all cases that source is zero-valued. Then, the currents leaving each node sum to give the value of the current source (q) at that node, as follows.
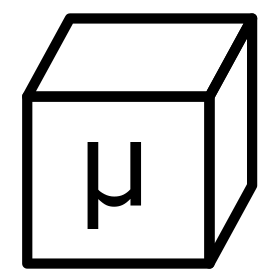
\( \begin{equation}V_{i,j} – V_{i+1,j} + V_{i,j} – V_{i-1,j} + V_{i,j} – V_{i,j+1} + V_{i,j} – V_{i,j-1} = R q_{i,j}\end{equation}\)
This can be simplified to the following. Let’s make it even simpler by setting the resistance value, R, to be 1 Ω. Anyone who has solved the Poisson equation by the finite difference method will recognise the following stencil.
\(\begin{equation}4V_{i,j} – V_{i+1,j} – V_{i-1,j} – V_{i,j+1} – V_{i,j-1} = q_{i,j}\end{equation} \)
So, we have the following matrix equation to solve, which is easily done using SciPy’s sparse matrix methods.
\( \textbf{A} \textit{v} = \textit{q} \)
In terms of the boundary conditions, we set a constant potential condition (V = 0) around the perimeter of the problem. As the grid gets bigger the boundary will be further away from current source and sink, so has a decreasing perturbation.
Solving the problem
First, we solve the problem on a small (11 x 11) grid. A current source of 1 A is placed at (4,4) with a corresponding current sink at (6,5). The resulting potential distribution is show below. Since a 1 A current is passed between the nodes, the resistance is V(4,4) – V(6,5) = 0.7453 Ω. The code can be found in the GitHub repo for this blog post. The analytic resistance has the remarkable value of 4/π-1/2 = 0.7732 Ω. The somewhat involved derivation of this result can be found here. In any case, we got close, even with rather few grid elements.

Let’s solve for various grid sizes and see if we can do any better. As expected, the result converges towards the analytic value as the grid size is increased.

It is perhaps interesting to look at the rate of convergence. Now we plot on a log-log plot the fractional error as a function of Δx,y = 1/Nx,y. Looking for the order of convergence we fit to Δxp, finding that the power of convergence is p = 2.16 i.e. there is second order convergence in Δx. This is also a familiar result from solving the Poisson equation.

It is now tempting to try other node pairs, find the numerical solution and try and guess what the analytic form would be. Also It would be fun to extend to other grids. However, that will have to wait for another day. Note that others have written about their numerical solutions to the Nerd Sniping comic, either modelling the circuit with SPICE or using a similar approach to that presented here.