‘Evidently, the makers of scent owe their livelihood to close encounters, wind and/or convective flow’. Those are the Feynman-esque words of the late Prof. Howard Berg, when discussing the diffusion of perfume in his 1993 book Random Walks in Biology (RWB). While diffusion contributes to molecule transport there and elsewhere, other effects can mask it. This doesn’t mean that diffusion is unimportant – consider how heat is transported out of an integrated circuit or how a plant transpires. However, it can be challenging to isolate diffusion from flow-phenomena such as convection. Here, I follow Prof. Berg’s recipe in order to measure diffusion coefficients. Partly, I was inspired by his wonderful book. But also, I have used diffusion coefficients, particularly of DNA, in many simulations. And see this blog-post for a simulation of thermal diffusion. As an experimental physicist it was time that I attempted a measurement of D!
Materials
Hardware
The containers for the diffusion experiment are 12 mm diameter glass test-tubes. I 3d-printed a support assembly in PLA and fixed it to a wooden base. The test-tubes were imaged by the Raspberry Pi (RPi) Camera Module 2 connected to a RPi 3 B+. The camera was set about 20 cm back from the test-tube support and affixed to the same base and its focus was manually adjusted.

It was important to maintain constant illumination, so the RPi also controlled a home-made back-illuminator. This comprised a number of white LEDs and a driver circuit. The light was guided by a sheet of clear acrylic plastic and diffused (!) by a sheet of opal acrylic. In order to remove the effect of ambient light, the whole assembly was placed in a box. The RPi was programmed to, every 12 minutes for several days, turn on the illuminator and take a photograph.
I used several colours of liquid food dye as the diffuser. The green dye shown here is from a supermarket in the UK. According to the ingredients, it contains Curcumin and a copper complex of Chlorophyllin as the dyes.
Software
A python script running on the RPi controls the camera and illuminator with the timing taken care of by the APScheduler module. A further sequence of scripts perform the data analysis and eventually fit the diffusion coefficients. The scripts can be found in this GitHub repository.
Methods
Filling the test-tubes
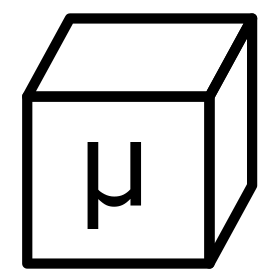
The test-tubes were 2/5 filled with tap water. A further 2/5 of 1 percent sugar solution was carefully poured in down the side of the glass. The sugar solution sinks to the bottom because of its greater density. We have two layers in the solution that, over the course of weeks, gradually merge together. In RWB it is mentioned that the diffusion coefficient (or diffusivity) of sucrose is about 500 μm2/s. Using <x2> = 2Dt we see that it will take about t = 50,000*50,000/2/500/3600/24 = 29 days for the sucrose to diffuse throughout the approximately 5 cm of liquid in the test-tube.
As described in RWB, the sugar gradient is important for several reasons. First, it provides a density gradient allowing the food dye to find its position of neutral buoyancy (so it doesn’t just sink to the bottom). And second, it stops convection which otherwise would be the main molecule transport process and mask diffusion (as with the perfume). Why does it stop convection? You can imagine a small volume element within the solution getting hotter than its surroundings and therefore expanding and lowering its density. In the presence of a density gradient it just rises to a new position of neutral buoyancy, rather than going all the way to the top.
Adding the food colouring
After setting up the sugar gradient, I put the food dye in a syringe and added a tiny drop to the solution about half way down. It was tricky to add a sufficiently small drop of food dye but possible with a bit of practise. If too much green food colouring is added the solution becomes almost completely opaque to the red and blue components of the white light. And this makes the extraction of the concentration profile difficult.
Results
I’ll start by showing photographs after 1 and 10 hours of the experiment. The images have been cropped and annotated (using the Python Pillow module) but no additional processing has been done on them. The food colouring has spread out, let’s assume by diffusion, but we need to find a way of quantifying this.


Choosing the colour channel
In order to fit to the colour profiles, I separate the 1 hour photograph (again using Pillow) into its red, green and blue components (figure below). As you would expect for a green dye, it mostly transmits green light but absorbs red and blue light. The greatest absorption is in the blue. A quick search for the absorption spectra for Curcumin and Chlorophyllin supports this behaviour. Curcumin has a broad absorption peak at around 425 nm (blue) and Chlorophyllin absorbs strongly in the blue and less strongly in red. Unfortunately, as so often, good references are behind paywalls.

Let’s look at vertical line scans for each colour channel (through the middle of the left test-tube). This (figure below) is again the 1 hour data, and it shows that the blue channel saturates. Hence, we have the choice of fitting to either the green or red channel. As we have a stronger signal in the red, I choose this one for further analysis.

Gaussian fits to the concentration profile
So now, taking a vertical line-scan though the red channel for each one of the test-tubes we are able to observe the evolution of the dye concentration profile. In the figure below, I plot the profile for the left test-tube each hour for the first 10 hours. The data points are shown in blue and Gaussian fits to the data in red. Actually the fit is to a straight line + a Gaussian, to account for the background slope. This slope is due to the non-constant intensity of light from the back-illuminator. The middle and right samples show similar behaviour.

The diffusion coefficient
From the Gaussian fits we extract the variance (σ2) at each time. Then plotting the variance against time (below) we see the linearity that is characteristic of diffusion and supports the fact that we are observing a diffusive process. And finally performing a linear fit to these experimental data points we are able to measure the diffusion coefficients. The relation between variance and diffusivity is as follows: σ2 = 2Dt. Using this we find diffusivity values for the left, middle and right test-tubes of 349 μm2/s, 336 μm2/s and 356 μm2/s. In order to translate pixels into mm, I used the known diameter of the test-tube (12 mm) and measured how many pixels this was across (80).

Discussion
It was encouraging to see how close the values of diffusivity were for the three samples. But of course random errors are one thing and systematic errors quite another. Some obvious places to look for systematic errors are in the calibration of pixels to distance, the parallax in the photographs and the imprecise setting up of the sugar gradient. There may be more.
In repeating this experiment, it would be good to choose a single molecule dye with a well measured diffusivity and to precisely setup a linear or exponential sugar gradient as described in RWB. It will also be interesting to compare the measured value for a given dye with other techniques.
I had the feeling in writing-up the experiment that it would make a superb undergraduate practical, or even a longer piece of project work. Perhaps you already have something similar in your institution? I’d be interesting to hear how you measure diffusion coefficients. Also, very happy to provide more details in case you are interested to set-up an experiment of this kind. Finally, thank you to Prof. Berg for writing RWB.