A while ago now I applied for an undergraduate place to study physics at the University of Oxford. In the interview I was asked a question about the relative cooking times of chickens and turkeys. My reasoning at the time was that heat went in at the surface but needed to raise the temperature of the volume. Imagining both the chicken and turkey to be spherical, the cooking time should go something like its weight to the power 2/3. Another reasonable answer would be that the cooking time goes like the weight. This question continues to perplex me. What would have been the best answer to give for a 17 year-old who only knows some basic physics and mathematics?
I thought it would be interesting to revisit the question, now knowing a little more about diffusion. Also, as this is a physics question and not a cooking one, please don’t use any of the analysis here for your Christmas/Thanksgiving dinner!
Let’s start by making the following assumptions. That heat transport within the turkey/chicken takes place by diffusion. That the oven leads to a constant temperature boundary condition at the surface of the bird. That the shape of each can be approximated by a solid sphere (cue usual jokes about physicists) with the thermal properties of water. That we don’t need to consider any latent heat e.g. due to liquid-gas phase changes. So then we are left with the solution of the radial term of the diffusion equation in spherical polar coordinates.
\( \begin{equation}
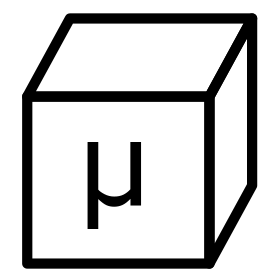
\frac{1}{r^2}\frac{\partial}{\partial r} (r^2\frac{\partial T}{\partial r}) = \frac{\partial T}{\partial t}
\end{equation} \)
I am going to numerically solve this equation by the finite difference method with a derivative boundary condition at the centre \( \frac{\partial T}{\partial r}=0\). Also there will be a constant temperature boundary condition at the surface. The code is available on GitHub as usual. Usefully, an exact solution is also available in Carslaw and Jaeger’s book (conduction of heat in solids) allowing us to verify the numerical solution. Below, we look at a comparison of the analytic and numerical solutions for a ‘chicken’ of radius 10 cm, left for 1 hour in an oven at 200 C. The forward Euler method was used with a time-step of 1 s and we see good agreement between the solutions. We would be in a position to use the L2 norm between the analytic and numerical solutions to optimise simulation parameters but let’s not do that today.

Sticking with the 10 cm chicken, we can look at the spatial distribution of temperature as a function of time. The resulting set of curves (one trace per hour) is seen below and corresponds to what one might expect. At a glance the cooking time looks to be approximately 2 hours which tallies with reality.

Now we are in a position to compare a chicken and a turkey. I am going to double the radius to 20 cm to represent the turkey, corresponding to 8 times the chicken’s weight. We also need a way to determine whether it is cooked. According to the USDA, the temperature of the meat should be 165 F (74 C). So let’s require this to be the case in the centre of each. And we will take a time trace of the temperature at the centre, looking for this condition to be met. We find that the 10 cm chicken takes slightly over 2 hours, while the turkey takes a little under 9 hours.

The ratio of the cooking time clearly doesn’t go as the weight (8 x). How does it compare to the surface area to volume ratio approach? Actually that gives a ratio 4.0, which is pretty close to the cooking time ratio (4.5) we get from solving the PDE. So perhaps this is the answer that the interviewer was looking for after all. To be honest, I was not expecting the naive approach to be so good. It shows the value of checking our simulations against even very simple estimates.